Measuring Code Complexity and Performance with examples

Software development is a process that not only demands proficiency in various coding languages but also an understanding of specific…

Luis Soares

02 Aug 2023 — 4 min read

Software development is a process that not only demands proficiency in various coding languages but also an understanding of specific theoretical principles that can drastically affect a program’s performance.

One of the most critical concepts in this realm is the Big O notation, a mathematical notation that describes the limiting behavior of a function, particularly when the argument tends towards a specific value or infinity. This notation is an instrumental tool used in computer science to describe an algorithm’s performance or complexity.

Understanding the Big O Notation

The Big O notation provides a high-level understanding of an algorithm’s time complexity, which is the computational complexity that describes the amount of computer time taken by an algorithm to run, as a function of the size of the input to the program.

It essentially answers the question: how does the run-time grow as the size of the input grows? This question is vital because it allows software developers to assess the efficiency of algorithms and identify potential bottlenecks or areas for improvement.

It’s crucial to note that Big O notation doesn’t measure the speed of an algorithm. Instead, it measures how quickly the run-time grows, based on the input size.

The Different Levels of Big O Notation

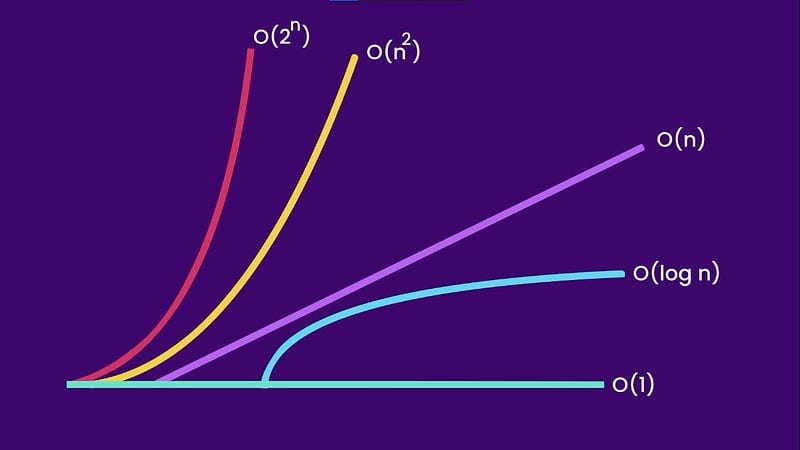
There are different levels of Big O notation that each represent different levels of complexity:

O(1): Also known as constant time complexity. No matter the size of the input, the time to complete the task remains the same. A typical example is accessing an element from an array using an index.
O(n): This is linear time complexity. The time to complete the task grows linearly with the size of the input. An example is looping through an array to find a specific value.
O(n²): This is quadratic time complexity. The time to complete the task is proportional to the square of the input size. Common examples include nested loops or bubble sort algorithm.
O(log n): Also known as logarithmic time complexity. The time to complete the task increases logarithmically with the input size. This is seen in algorithms like binary search.
O(n log n): This is linearithmic time complexity, where the time to complete the task increases linearly and logarithmically for small and large inputs respectively. Efficient sorting algorithms like mergesort or quicksort exhibit this kind of time complexity.

Examples of Big O Notation

Let’s look at some examples in Python:

O(1) — Constant Time Complexity

def get_first_item(items): 
    return items[0] 
 
print(get_first_item([1, 2, 3, 4, 5]))

In this example, no matter the size of the list, we always use the same amount of time to retrieve the first item.

O(n) — Linear Time Complexity

def find_item(items, element): 
    for item in items: 
        if item == element: 
            return True 
    return False 
 
print(find_item([1, 2, 3, 4, 5], 3))

Here, the time to find an item grows linearly with the size of the list. In the worst case scenario, we would have to look at every item in the list.

O(n²) — Quadratic Time Complexity

def bubble_sort(items): 
    n = len(items) 
 
    for i in range(n): 
        for j in range(0, n - i - 1): 
            if items[j] > items[j+1]: 
                items[j], items[j+1] = items[j+1], items[j] 
 
numbers = [64, 34, 25, 12, 22, 11, 90] 
bubble_sort(numbers) 
print(numbers)

In this example, for each item in the list, we’re comparing it to every other item. This means that the time complexity grows quadratically with the size of the input list.

O(log n) — Logarithmic Time Complexity

def binary_search(items, element): 
    low = 0 
    high = len(items) - 1 
 
    while low <= high: 
        mid = (low + high) // 2 
        guess = items[mid] 
        if guess == element: 
            return mid 
        elif guess > element: 
            high = mid - 1 
        else: 
            low = mid + 1 
    return None 
 
my_list = [1, 3, 5, 7, 9] 
print(binary_search(my_list, 3))

In the binary search algorithm, the list is divided into half at each step until the search item is found. In the worst case scenario, the time complexity is logarithmic, meaning the run-time increases logarithmically with the size of the input.

O(n log n) — Linearithmic Time Complexity

def merge_sort(items): 
    if len(items) <= 1: 
        return items 
 
    mid = len(items) // 2 
    left_half = items[:mid] 
    right_half = items[mid:] 
 
    return merge(merge_sort(left_half), merge_sort(right_half)) 
 
def merge(left, right): 
    merged = [] 
    left_index = 0 
    right_index = 0 
 
    while left_index < len(left) and right_index < len(right): 
        if left[left_index] < right[right_index]: 
            merged.append(left[left_index]) 
            left_index += 1 
        else: 
            merged.append(right[right_index]) 
            right_index += 1 
 
    merged.extend(left[left_index:]) 
    merged.extend(right[right_index:]) 
    return merged 
 
numbers = [38, 27, 43, 3, 9, 82, 10] 
print(merge_sort(numbers))

In the merge sort algorithm, the list is divided into two halves, each of them is sorted and then merged. This operation is performed recursively, creating a divide-and-conquer strategy that makes the algorithm highly efficient for large datasets.

Real-World Trade-Offs

When dealing with real-world applications, one has to bear in mind that there may be better strategies than choosing an algorithm based solely on its Big O notation. Some algorithms with a ‘better’ Big O notation might perform poorly in certain circumstances. For instance, an algorithm with a time complexity of O(n) might be faster than an algorithm with a time complexity of O(log n) for small input sizes due to the simplicity of the operations involved or caching effects.

In conclusion, while understanding the Big O notation and its implications on an algorithm’s time complexity is crucial, it’s also essential to consider the specific constraints and requirements of the problem you’re trying to solve. This could involve considering factors such as the input data’s nature and size, the available hardware, and the specific use case to choose the most appropriate algorithm for the task.

Stay tuned, and happy coding!

Visit my Blog for more articles, news, and software engineering stuff!

Follow me on Medium, LinkedIn, and Twitter.

All the best,

Luis Soares

#cleancode #algorithm #optimization #complexity #performance #bigo #softwaredevelopment #coding #software #development #building #architecture